1M-Fonctions

Documents de cours

• Série 16 à 21

Pages liées

• Astuces du chapitre
• Exemples du chapitre
• Définitions du chapitre
• Automatismes QR-codes sur les fonctions

Liste des compétences étudiées

• Établir et compléter un tableau de valeurs en utilisant la calculatrice (cours du 6.1.25)
• Déterminer si une fonction passe par un point donné en évaluant la fonction (cours du 6.1.25)
• Déterminer la pente et l'ordonnée à l'origine d'une fonction affine à partir de son expression algébrique (cours du 6.1.25)
• Représenter graphiquement une fonction affine (cours du 6.1.25)
• Distinguer les différentes écritures algébriques d'une droite : équation cartésienne, équation réduite (cours du 9.1.25)
• Déterminer l'expression algébrique d'une droite à partir de sa représentation graphique (cours du 9.1.25)
• Déterminer l'expression algébrique d'une droite à partir de deux points (cours du 9.1.25)
• Connaître les conditions de parallélisme et de perpendicularité de deux droites (cours du 13.1.25)
• Déterminer l'expression algébrique d'une droite à partir de conditions données sur la pente et un point (cours du 13.1.25)
• Déterminer si trois points sont alignés (cours du 13.1.25)
• Calculer le point d'intersection de deux droites (cours du 16.1.25)
• Établir un tableau de signes d'une parabole (cours du 23.1.25)
• Réaliser une étude complète d'une parabole (cours du 23.1.25)
• Déterminer le(s) point(s) d'intersection d'une droite et d'une parabole (cours du 27.1.25)
• Déterminer le(s) point(s) d'intersection de deux paraboles (cours du 27.1.25)
• Calculer la distance entre deux points (cours du 27.1.25)
• Déterminer le milieu d'un segment (cours du 27.1.25)
• Déterminer le sommet d'une parabole (cours du 30.1.25)
• Déterminer les zéros d'une parabole (cours du 30.1.25)
• Déterminer l'axe de symétrie d'une parabole (cours du 30.1.25)
• Utiliser les différentes écritures d'une parabole : forme générale, forme canonique, forme factorisée (cours du 30.1.25)
• Appliquer les notions de distance et de milieu pour résoudre des problèmes (cours du 3.2.25)
• Modéliser des problèmes par des fonctions du second degré (cours du 6.2.25)
• Résoudre une situation d'optimisation en utilisant la notion de maximum ou de minimum d'une parabole (cours du 6.2.25)

Semaine 21

Cours du 3.2.25

Compétences

• Appliquer les notions de distance et de milieu pour résoudre des problèmes

En utilisant les propriétés des quadrilatères, on peut déterminer si un quadrilatère défini par quatre points est un carré ou un rectangle.

Déterminer si quatre points forment un carré

Il y a plusieurs possibilités pour déterminer si quatre points forment un carré, en voici une:
On vérifier que les quatre côtés ont le même longueur et qu'un des côté est perpendiculaire à un autre (ce qui permet de s'assurer que les quatre autres angles sont des angles droits).
En utilisant un raisonnement similaire, on peut déterminer si un quadrilatère en un rectangle.

Déterminer si un quadrilatère est un carré

Montrer que le quadrilatère $ABCD$ avec $A(0;-1), B(-3;1), C(-5;-2)$ et $D(-2;-4)$ est un carré. On commence par vérifier que les quatre côté ont la même longueur. Pour cela on calcule $\text{dist}(A;B)$, $\text{dist}(B;C)$, $\text{dist}(C;D)$ et $\text{dist}(D;A)$. On a
$\begin{aligned} \text{dist}(A;B)&=\sqrt{(-3-0)^2 +(1+1)^2 }=\sqrt{13}\\ \text{dist}(B;C)&=\sqrt{(-5+3)^2 +(-2-1)^2 }=\sqrt{13}\\ \text{dist}(C;D)&=\sqrt{(-2+5)^2 +(-4+2)^2 }=\sqrt{13}\\ \text{dist}(D;A)&=\sqrt{(0+2)^2 +(-1+4)^2 }=\sqrt{13}\\ \end{aligned}$
On vérifie ensuite que le quadrilatère contient au moins un angle droit, c'est-à-dire que la droite $AB$ est perpendiculaire à la droite $AD$. On a que la pente entre $AB$ vaut $-\dfrac{2}{3}$ et la pente entre $AD$ vaut $\dfrac{3}{2}$, donc les deux droites sont bien perpendiculaire, ce qui montre que $ABCD$ est un carré.

Exercice résolu en cours

• Prouver que le quadrilatère $ABCD$ avec $A(-5;0), B(0;-1), C(1;4)$ et $D(-4;5)$ est un carré.

Ressources

• Question du début de cours

Cours du 6.2.25

Compétences

• Modéliser des problèmes par des fonctions du second degré
• Résoudre une situation d'optimisation en utilisant la notion de maximum ou de minimum d'une parabole

Voici les problèmes résolus en cours :

Exercice résolu en cours

• Pour quelle valeur de $x$ l'expression $x^2 +(x+1)^2 +(x+2)^2$ est-elle minimale, et que vaut alors cette expression ? Interpréter graphiquement.
• Un terrain se trouve en bordure d'une rivière rectiligne. On désire délimiter une zone rectangulaire le long de la rivière à l'aide d'une barrière ayant une longueur totale de 120 mètres. Le côté de la zone le long de la rivière n'a pas besoin de barrière. Quelle est l'aire maximale possible de la zone délimitée par la barrière et la rivière ?
• Une agence de voyage organise une excursion. Le prix du billet a été fixé à 60 CHF, mais la compagnie a consenti, dans le cas où plus de 100 personnes feraient le voyage, à baisser le prix de chaque billet de 25 cts par personne additionnelle. Sachant qu'il en coûte 1000 CHF à l'agence pour transporter les 100 premiers passagers et 15 CHF par passager additionnel, trouver le nombre de passagers pour lequel le bénéfice net de la compagnie est maximal. Interpréter graphiquement.

Ressources

• Question du début de cours

Semaine 20

Cours du 27.1.25

Compétences

• Déterminer le(s) point(s) d'intersection d'une droite et d'une parabole
• Déterminer le(s) point(s) d'intersection de deux paraboles
• Calculer la distance entre deux points
• Déterminer le milieu d'un segment

Théorie

Point d'intersection entre deux paraboles

Afin de déterminer le point d'intersection entre deux paraboles, on égalise les deux fonctions et on résout l'équation obtenue, comme pour les droites.

Point d'intersection entre deux paraboles

On cherche à déterminer le point d'intersection entre les paraboles $f(x)=-3x^2+x-6$ et $g(x)=-6x^2-2$.
On égalise les deux fonctions et on résout l'équation obtenue. On a $-3x^2 +x-6=-6x^2-2$.
On résout cette équation et on obtient $x_1=-\dfrac{4}{3}$ et $x_2=1$.
On substitue ces valeur dans l'une des deux fonctions pour obtenir l'ordonnée des points d'intersection.
On calcule $f\left(-\dfrac{4}{3}\right)=-10$ et $f(1)=-8$.
On a $f\cap g=\left\{\left(-\dfrac{4}{3};-10\right);(1;-8)\right\}$.

Exercices résolus en cours

• Déterminer les points d'intersections entre deux paraboles

Définition (distance entre deux points):

La distance entre deux points $A(x_1;y_1)$ et $B(x_2;y_2)$ est donnée par la formule \[\text{dist}(A;B)=\sqrt{(x_1-x_2)^2 +(y_1-y_2)^2 }.\]

Distance entre deux points

La formule de la distance entre deux points est une application directe du théorème de Pythagore.

Définition (milieu d'un segment):

Le milieu d'un segment $[AB]$ est le point $M$ tel que \[\text{dist}(A;M)=\text{dist}(M;B).\]

Milieu d'un segment

Si $A(x_1;y_1)$ et $B(x_2;y_2)$ sont deux points, le milieu $M$ du segment $[AB]$ est donné par les coordonnées \[M=\left(\dfrac{x_1+x_2}{2};\dfrac{y_1+y_2}{2}\right).\]

Exercices résolus en cours

• Déterminer la distance entre les points $A$ et $B$, et entre les points $C$ et $D$ avec $A(1;3)$, $B(4;9)$, $C(-3;1)$ et $D(-2;-4)$.
• Déterminer le coordonées du milieu du segment $[AB]$ et du segment $[CD]$ avec $A, B, C, D$ donnés ci-dessus.

Définition (hauteur issue d'un sommet):

Soit le triangle $ABC$. La hauteur issue du sommet $A$ est la droite passant par $A$ perpendiculaire au côté opposé à $A$ (ici au côté $BC$). Par abus de langage, la longueur de la hauteur est la longueur du segment $[AH]$ où $H$ est la point d'intersection entre de la hauteur et le côté oppoés à $A$.

Hauteur issue d'un sommet

Soit le triangle $ABC$. Pour déterminer la hauteur issue du sommet $A$, on détermine l'équation de la droite du côté $BC$. Puis on détermine l'équation de la droite passant par $A$ et perpendiculaire à la droite $BC$.
Pour déterminer la longueur de la hauteur, on détermine le point d'intersection entre la hauteur et $BC$, puis on détermine la distance séparant $A$ et ce point d'intersection.

Déterminer la hauteur issue d'un sommet

Soit le triangle $ABC$ avec $A(0;1)$, $B(-2;3)$ et $C(-8;7)$. Déterminer la longueur de la hauteur issue de $A$.
On a que a droite $BC$ a comme équation réduite $y=-\dfrac{2}{3}x+\dfrac{5}{3}$. On cherche à présent la droite perpendiculaire à $BC$ passant par $A$. La pente de cette droite vaut $\dfrac{3}{2}$ et on détermine son ordonnée à l'origine en utilisant l'information qu'elle passe par $A$. Donc $1=\dfrac{3}{2}\cdot 0+b$ d'où $b=1$.
Ainsi, l'équation de la droite est $y=\dfrac{3}{2}x+1$.
On détermine le point d'intersection entre cette droite et $BC$ pour obtenir $H(\dfrac{4}{13};\dfrac{19}{13})$. La distance entre $A$ et $H$ est donnée par $\text{dist}(A;H)=\sqrt{(\dfrac{4}{13}-0)^2 +(\dfrac{19}{13}-1)^2 }=2\dfrac{\sqrt{13}}{13}$.

Exercices résolus en cours

• Déterminer la longueur hauteur du triangle $ABC$ issue de $A$ où $A(0;1)$, $B(-2;3)$ et $C(-8;7)$.
• Choisir trois points non colinéaire dans le plan, calculer l'aire du triangle définit par ces points.

Ressources

• Question du début de cours
• Introduction à l'optimisation

Cours du 30.1.25

Ressources

• Question du début de cours
• Devoir à rendre

Semaine 19

Cours du 20.1.25

Compétences

• Déterminer le sommet d'une parabole
• Déterminer les zéros d'une parabole
• Déterminer l'axe de symétrie d'une parabole
• Utiliser les différentes écritures d'une parabole : forme générale, forme canonique, forme factorisée

Théorie

Définition (parabole):

La courbe représentative d'une fonction du deuxième degré, c'est-à-dire d'une fonction de la forme $f(x)=ax^2+bx+c$ où $a\neq 0$ et $a,b,c\in \mathbb{R}$ s'appelle une parabole. Une parabole peut s'écrire sous différentes formes : forme générale, forme canonique, forme factorisée.

Avant d'introduire ces trois écritures, nous devons définir les notions suivantes.

Définition (zéros):

Les zéros d'une parabole sont les points d'intersection de la parabole avec l'axe des abscisses. Ce sont les solutions de l'équation $ax^2+bx+c=0$.

Définition (sommet):

Le sommet d'une parabole, noté $S$, est le point de la parabole qui a l'ordonnée minimale (si $a>0$) et maximale (si $a<0$).

Sommet d'une parabole

Pour une parabole $f(x)=ax^2+bx+c, a\neq 0$, le sommet est donné par les coordonnées $\left(-\dfrac{b}{2a};f\left(-\dfrac{b}{2a}\right)\right)$.

Définition (axe de symétrie):

L'axe de symétrie d'une parabole $f$ est la droite d'équation $x=s$ tel que $f(s-t)=f(s+t), \forall t \in \mathbb{R}$.

Axe de symétrie d'une parabole

Pour une parabole $f(x)=ax^2+bx+x, a\neq 0$, l'axe de symétrie est donné par l'équation $x=-\dfrac{b}{2a}$.

Définition (forme générale d'une parabole):

La forme générale d'une parabole $f$ est donnée par $f(x)=ax^2+bx+c$.

Définition (forme canonique d'une parabole):

La forme canonique d'une parabole $f$ est donnée par $f(x)=a(x-\alpha)^2+\beta$ où $(\alpha;\beta)$ est le sommet de la parabole.

Définition (forme factorisée d'une parabole):

La forme factorisée d'une parabole $f$ est donnée par $f(x)=a(x-x_1)(x-x_2)$ où $x_1$ et $x_2$ sont les zéros de la parabole.

Forme canonique

Pour passer de la forme générale à la forme canonique, on peut utiliser deux méthodes :
1) Calcul du sommet par la formule $S\left(-\dfrac{b}{2a};f\left(-\dfrac{b}{2a}\right)\right)$. Puis substition dans la forme canonique: \[f(x)=\left(x+\dfrac{b}{2a}\right)^2+f\left(-\dfrac{b}{2a}\right)\]
2) Complétion du carré :
$\begin{aligned} f(x)&=ax^2+bx+c\\ &=a\left(x^2+\dfrac{b}{a}x\right)+c\\ &=a\left(x^2+ \dfrac{b}{a}x+\dfrac{b^2 }{4a^2 }-\dfrac{b^2 }{4a^2 }\right)+c\\ &=a\left(x+\dfrac{b}{2a}\right)^2 -\dfrac{b^2 }{4a}+c\\ &=a\left(x+\dfrac{b}{2a}\right)^2 -\dfrac{b^2 -4ac}{4a}\ \end{aligned}$

Forme factorisée

Pour passer de la forme générale à la forme factorisée d'une parabole $f$, on utilise les zéros de la parabole. Les zéros sont les solutions de l'équation $ax^2+bx+c=0$.
Si $\Delta\geq 0$. On a $x_1=\dfrac{-b-\sqrt{b^2-4ac}}{2a}$ et $x_2=\dfrac{-b+\sqrt{b^2-4ac}}{2a}$. Ainsi, la forme factorisée est donnée par \[f(x)=a(x-x_1)(x-x_2).\]

Différentes écritures d'une parabole

Cette anmation permet de visualiser les différentes écritures d'une parabole, de comprendre les relations entre elles et de visualiser les points particuliers de chaque écriture.

Exercices

Exercices résolus en cours

• Passer de l'écriture générale à la forme canonique.
• Pour les paraboles suivantes, déterminer les zéros de la parabole, l'axe de symétrie, la forme canonique et la forme factorisée
  • $f(x)=3x^2-2x-1$
  • $g(x)=-\dfrac{2}{3}x^2+4x-3$
  • $h(x)=x^2-4x+5$

Ressources

• Question du début de cours

Cours du 23.1.25

Compétences

• Établir un tableau de signes d'une parabole
• Réaliser une étude complète d'une parabole

Théorie

Dans cette partie, nous verrons comment utiliser ce que nous avons vu précédemment pour réaliser une étude complète d'une parabole. Nous commençons par organiser les données dans un tableau de signes.

Définition (tableau de signes):

Un tableau de signes est un tableau qui permet de lire rapidement la variation des signes d'une fonction.

Tableau de signes d'une paraboles

Pour réaliser un tableau de signes, on commence par déterminer les zéros de la parabole. On place sur la première ligne les zéros dans un tableau avec des bornes $-\infty$ et $+\infty$ aux extrémités. On évalue la parabole pour des valeurs dans les intervalles délimités par les zéros pour obtenir le signe de la parabole dans cet intervalle. On peut aussi utiliser nos connaissances sur les variations de la fonction pour déterminer les signes.

Tableau de signes d'une parabole

Établir un tableau de signes de la parabole $f(x)=x^2-3x+2$.
On note que le coefficient dominant, le coefficient $a$, de la parabole est positif. Ainsi, la parabole est convexe, donc positive aux extrémités.
1) On commence par déterminer les zéros de la parabole. On résout l'équation $x^2-3x-2=0$ pour obtenir $x_1=1$ et $x_2=2$.
2) On place les zéros dans un tableau et les signes $-\infty$ et $+\infty$ aux extrémités. On complète le tableau avec les signes.

Etude complète d'une parabole

Pour réaliser une étude complète d'une parabole, il faut:
1) Déterminer les zéros de la parabole
2) Déterminer le point d'intersection avec l'axe des ordonnées
3) Détermine ensuite l'axe de symétrie
4) Déterminer le sommet de la parabole
5) Déterminer la concavité et réaliser un tableau de signes
6) Utiliser les informations pour représenter graphiquement la parabole (en utilisant les points particuliers et le tableau de signes)

Etude complète d'une parabole

On va étudier la parabole $f(x)=-x^2+3x-2$.

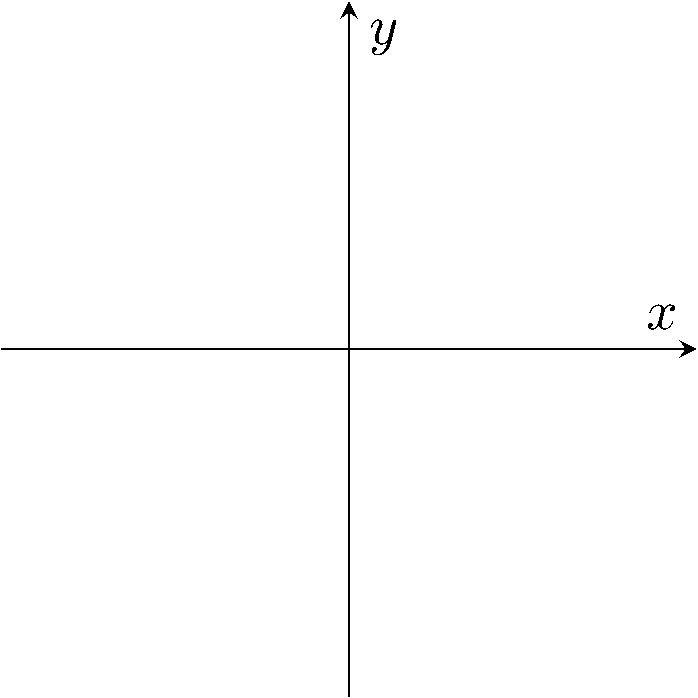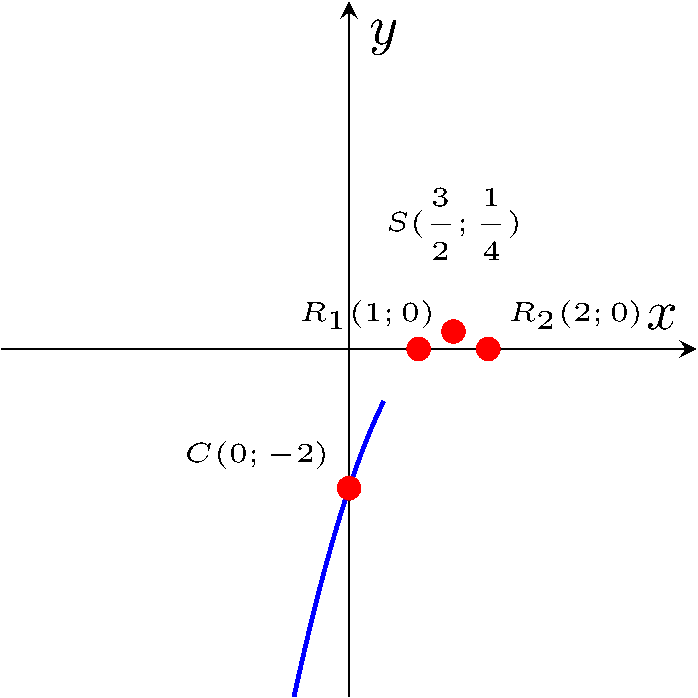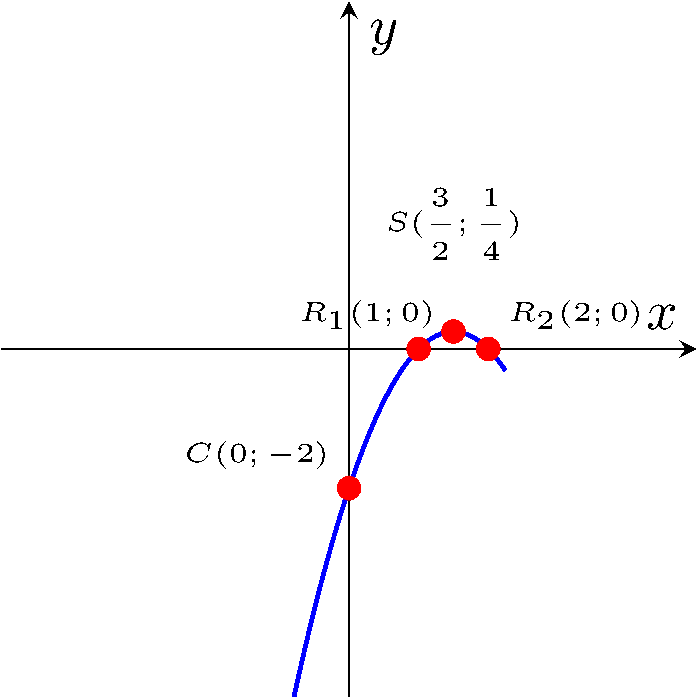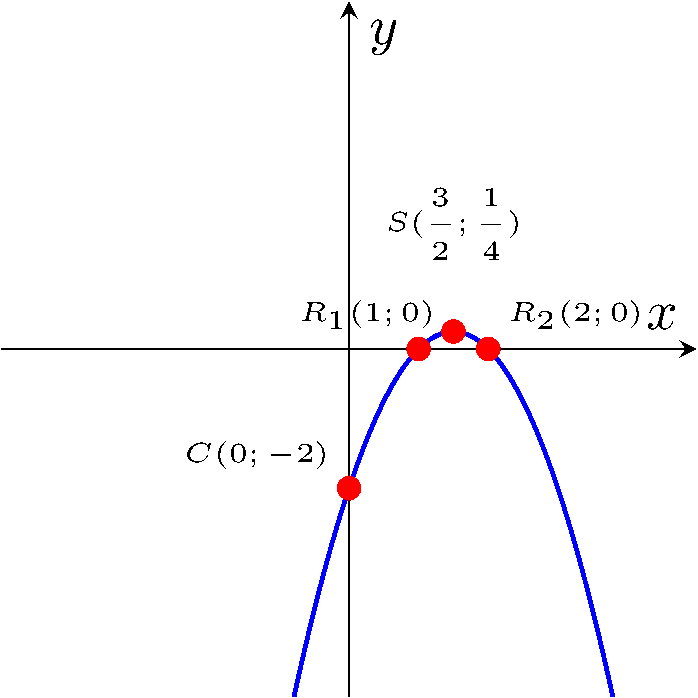
1) Les zéros de la parabole sont les solutions de l'équation $-x^2+3x+2=0$. On a $x_1=1$ et $x_2=2$, donc les points d'intersection avec l'axe des abscisses sont $R_1(1;0)$ et $R_2(2;0)$.

2) Le point d'intersection $C(0,f(0))$ avec l'axe des ordonnées est donné par $C(0,-2)$.

3) L'axe de symétrie est donné par $x=-\dfrac{b}{2a}$, donc $x=\dfrac{3}{2}$.

4) Le sommet est donné par les coordonnées $S\left(\dfrac{3}{2};f\left(\dfrac{3}{2}\right)\right)=S\left(\dfrac{3}{2};\dfrac{1}{4}\right)$.

5) La concavité est donnée par le signe du coefficient dominant. Le signe du coefficient dominant est $-1$, donc la parabole est concave. On réalise le tableau de signes en utilisant les zéros.

On trace ensuite le graphe de la parabole en utilisant les informations obtenues en plaçant les points d'intersection avec les axes, le sommet et en utilisant le tableau de signes.

Exercices

Exercices résolus en cours

• Réaliser un tableau de signes.
• Etude complète d'une parabole.

Ressources

• Question du début de cours

Semaine 18

Cours du 13.1.25

Compétences

• Connaître les conditions de parallélisme et de perpendicularité de deux droites
• Déterminer l'expression algébrique d'une droite à partir de conditions données sur la pente et un point
• Déterminer si trois points sont alignés

Théorie

Définition (parallèle):

Deux droites sont parallèles si elles ont la même pente.

Définition (perpendiculaire):

Deux droites sont perpendiculaires si le produit de leur pente vaut $-1$. Soient deux droites $d_1$ d'équation $y=ax+b$ et $d_2$ d'équation $y=cx+d$, alors les droite $d_1$ et $d_2$ sont perpendiculaires si et seulement si \[a\cdot c=-1.\]

Droites perpendiculaire

Le produit de la pente de droite perpendiculaire vaut $-1$, donc si $a\neq 0$ et $a'\neq 0$ sont les pentes de deux droites perpendiculaires, $a'=-\dfrac{1}{a}$.

Equation d'une droite perpendiculaire passant par un point

Déterminer l'équation de la droite perpendiculaire à $y=2x-1$ passant par le point $(3;4)$.
On note cette nouvelle droite $y=ax+b$. Il faut déterminer $a$ et $b$.
On commence par déterminer la pente $a$.
Par le critère de perpendicularité, $a\cdot 2=-1$, donc $a=-\dfrac{1}{2}$. Ainsi $y=-\dfrac{1}{2}x+b$.
Pour déterminer la valeur de $b$, on substitue le point $(3;4)$ dans l'équation. On a $4=-\dfrac{1}{2}\cdot 3 +b$ d'où $b=\dfrac{11}{2}$.
Ainsi, $y=-\dfrac{1}{2}x+\dfrac{11}{2}$ est l'équation réduite de la droite recherchée.

Définition (points alignés):

Trois points $A, B, C$ sont alignés si les pentes entre tous les couples de points est identique.

Points alignés

Pour vérifier si trois points $A, B, C$ sont alignés, il suffit de vérifier que $\text{pente}(A;B)=\text{pente}(A;C)$.

Points alignés :

Soient les points $A(1; 2)$, $B(2; 4)$ et $C(3; 6)$. Déterminer si $A, B, C$ sont alignés.
Calculons les pentes entre chaque couple de points.
On a $\text{pente}(A;B) = \dfrac{4-2}{2-1} = 2$ et $\text{pente}(A;C) = \dfrac{6-2}{3-1} = 2$.
Les pentes sont identiques, donc les points $A$, $B$ et $C$ sont alignés.

Exercices

Exercices résolus en cours

• Déterminer l'équation réduite d'une droite parallèle à $y=\dfrac{1}{3}x+1$.
• Déterminer l'équation réduite d'une droite perpendiculare à $y=\dfrac{1}{3}x+1$.
• Déterminer si les points suivants sont alignés.
• Déterminer l'équation d'une droite parallèle/perpendiculaire à une droite passant par un point donné.

Ressources

• Question du début de cours

Exercices supplémentaires

• Rappeler la condition sur les pentes de deux droites afin qu'elles soient parallèles ou perpendiculaires.
• Déterminer l'ensemble des droites parallèle à la droite d'équation $y=-\dfrac{3}{4}x-1$.
• Déterminer l'équation de la droite parallèle à la droite d'équation $y=\dfrac{1}{3}x+2$ passant par le point $(4;-2)$.
• Déterminer l'équation de la droite perpendiculaire à la droite d'équation $y=\dfrac{4}{5}x-3$ passant par le point $\left(\dfrac{1}{7};8\right)$.

Cours du 16.1.25

Compétences

• Calculer le point d'intersection de deux droites

Théorie

• Par définition le point d'intersection entre deux courbes est un point qui appartient aux deux courbes.

Point d'intersection

Soient deux courbes décrites par les fonctions $f$ et $g$.
Afin de déterminer les points d'intersection (s'il y en a) entre les deux courbes, on égalise leur expression et on résout l'équation ainsi obtenue \[f(x)=g(x)\] La solution de cette équation nous fournit la coordonnées de abscisse des possibles points d'intersection.
On substitue ensuite cette coordonnée dans l'une des deux expressions afin de calculer la coordonnée des ordonnées.
On peut choisir n'importe laquelle des deux courbes.

Points d'intersection de deux droites

Dans le cas particulier de deux droites $d_1:y=ax+b$ et $d_2:y=cx+d$, l'intersection $d_1\cap d_2$ est donnée par la solution du système d'équation \[\begin{cases} y&=ax+b\\y&=cx+d\end{cases}\] On peut résoudre ce système en commençant par égaliser les deux expressions pour obtenir une équation en une seule variable \[ax+b=cx+d\]

Point d'intersection

On procède comme suit pour calculer les point d'intersection de $f(x)=-x+4$ et $g(x)=x^2-2x-2$ (noté $f\cap g$). On égalise les deux expressions \[f(x)=g(x)\] \[ -x+4=x^2-2x-2.\] On résout l'équation et on obtient deux solution $x_1=-2$ et $x_2=3$. On déduit que $f\cap g$ contient deux points dont les coordonnées sont $(-2; ?)$ et $(3; ?)$. On évalue les coordonnées des abscisses dans l'une des deux courbes (on choisit la droite par simplicité) et on obtient la deuxième coordonnée : \[f(-2)=-(-2)+4=6\] et \[f(3)=-(3)+4=1\] Ainsi, $f\cap g=\{(-2;6);(3;1)\}$.

Exercices

Exercices résolus en cours

• Déterminer le point d'intersection de deux droites.
• Exercice d'appronfondissement : croisement.

Ressources

• Question du début de cours

Semaine 17

Cours du 6.1.25

Compétences

• Établir et compléter un tableau de valeurs en utilisant la calculatrice
• Déterminer si une fonction passe par un point donné en évaluant la fonction
• Déterminer la pente et l'ordonnée à l'origine d'une fonction affine à partir de son expression algébrique
• Représenter graphiquement une fonction affine

Théorie

Définition (fonction affine):

Une fonction est appelée affine si elle est de la forme $f(x)=ax+b$. Sous cette forme, le coefficient $a$ s'appelle la pente et le coefficient $b$ l'ordonnée à l'origine. Si $a=0$, on dit que la fonction est constante. Si $b=0$, on dit que la fonction est linéaire.

Une fonction affine correspond à une droite non verticale et toutes les droites non verticales peuvent être représentées par une fonction affine.

Représenter une fonction affine

Pour représenter une fonction affine, il suffit de déterminer deux points appartenant au graphe de la fonction, de les placer sur un repère et de les relier. On a l'habitude de placer un troisième point comme outil de vérification. On peut également représenter une fonction affine en utilisant sa pente et son ordonnée à l'origine.

Point appartenant au graphe d'une fonction

Un point $(A_x; A_y)$ appartient au graphe d'une fonction $f$ (noté $G_f$) si et seulement si $f(A_x)=A_y$.

Point appartenant au graphe d'une fonction

Le point $(2;8)$ appartient-il au graphe de $f(x)=3x+1$ ? Non, il n'appartient pas à $G_f$, car $f(2)=3\cdot 2+1=7\neq 8$. Par contre, le point $(0;1)$ appartient à $G_f$, car $f(0)=3\cdot 0+1=1$.

Ressources

• Question du début de cours
• Exercices 11 à 17 des séries.

• Tableau de valeurs avec la calculatrice

Exercices supplémentaires

• Rappeler la définition du graphe d'une fonction $f$.
• Déterminer si le point $A(3;16)$ appartient au graphe de $f(x)=3x^2-4x+1$.
• Compléter afin que le point $B(-;1)$ appartienne au graphe de $f(x)=3x^2-4x+1$.
• Déterminer la pente et l'ordonnée à l'origine de la fonction $g(x)=-x+\dfrac{3}{2}$ et de la fonction $h(x)=\dfrac{5-x}{3}$.
• Représenter graphiquement dans un même repère les fonctions $g$ et $h$.

Cours du 9.1.25

Compétences

• Distinguer les différentes écritures algébriques d'une droite : équation cartésienne, équation réduite
• Déterminer l'expression algébrique d'une droite à partir de sa représentation graphique
• Déterminer l'expression algébrique d'une droite à partir de deux points

Théorie

Définition (écritures d'une droite):

L'équation réduite d'une droite est donnée par $y=ax+b$ où $a$ est la pente et $b$ l'ordonnée à l'origine. L'équation cartésienne d'une droite est donnée par $Ax+By+C=0$ avec $A,B,C \in \mathbb{R}$. Cette forme rappelle les équations des systèmes d'équations linéaires à deux inconnues. On passe d'une forme à une autre en isolant la variable $y$ ou en comparant l'expression à $0$.

Définition (pente):

La pente est définie comme le rapport de la variation verticale et de la variation horizontale \[\text{pente}=\dfrac{\Delta \text{ vert.}}{\Delta \text{ hor.}}.\]

Formule de la pente

La pente entre deux points $A(A_x;A_y)$ et $B(B_x;B_y)$ vaut \[\text{pente }(A;B)=\dfrac{A_y-B_y}{A_x-B_x}.\] Cette formule ne fait du sens que si $A_x\neq B_x$. On remarque également que cette formule est symétrique, $\text{pente }(A;B)=\text{pente }(B;A)$.

Exercices

Exercices résolus en cours

• Mettre sous forme cartésienne la droite d'équation : $y=\dfrac{3}{4}x+3$.
• Mettre sous forme réduite la droite d'équation : $0=-2y+3x-1$.
• Peut-on représenter la droite $x=3$ par une fonction affine ? Expliquer.
• Déterminer l'expression réduite d'une droite à partir de sa représentation graphique.
• Déterminer la pente d'une droite passant par deux points.
• Déterminer l'expression algébrique d'une droite connaissant sa pente et un point.
• Déterminer l'expression algébrique d'une droite passant par deux points.

Ressources

• Question du début de cours

Exercices supplémentaires

• Rappeler la différence entre l'équation cartésienne et l'équation réduite d'une droite.
• Déterminer l'expression réduite de la droite passant par les points $A(0;-5)$ et $B(-3;-1)$.
• Déterminer l'expression réduite des droites $(d_1)$ et $(d_2)$.